Flatlandia: dalla prima alla quarta dimensione – Ecco come ci apparirebbero le altre dimensioni se le visitassimo

Immaginare 4 dimensioni spaziali

Quando abbiamo parlato della teoria delle stringhe, seguendo il ragionamento siamo arrivati a intuire che lo spazio attorno a noi non può essere fatto soltanto dalle tre dimensioni che conosciamo – larghezza, lunghezza, altezza – ma ne devono esistere almeno 10. In caso contrario, la teoria delle stringhe non funzionerebbe.

Se siete interessati, vi invito a rivedere il video di Brian Greene presente nell’altro articolo, che vi spiega in modo chiaro e pulito la teoria delle stringhe.

Immaginarsi le altre 7 dimensioni spaziali che ci circondano è estremamente difficile, per il semplice fatto che non ne abbiamo percezione. Vediamo un attimo di capire perché è difficile (anzi, impossibile) per noi umani immaginare un qualsiasi oggetto in quattro dimensioni. Prendiamo come esempio una figura geometrica per eccellenza: il quadrato.

Immaginiamo di avere tante tavole di legno quadrate, della stessa misura. Se vi dicessi di creare un cubo a partire da queste, non avreste problema a farlo, perché vi basterebbe impilare tanti quadrati uno sopra all’altro fino a quando non si forma il cubo voluto. In questo caso, avete «traslato» il quadrato verso una direzione a lui perpendicolare, cioè siete passati dalla seconda dimensione (il quadrato ha solo altezza e larghezza) alla terza dimensione (aggiungendo l’altezza).

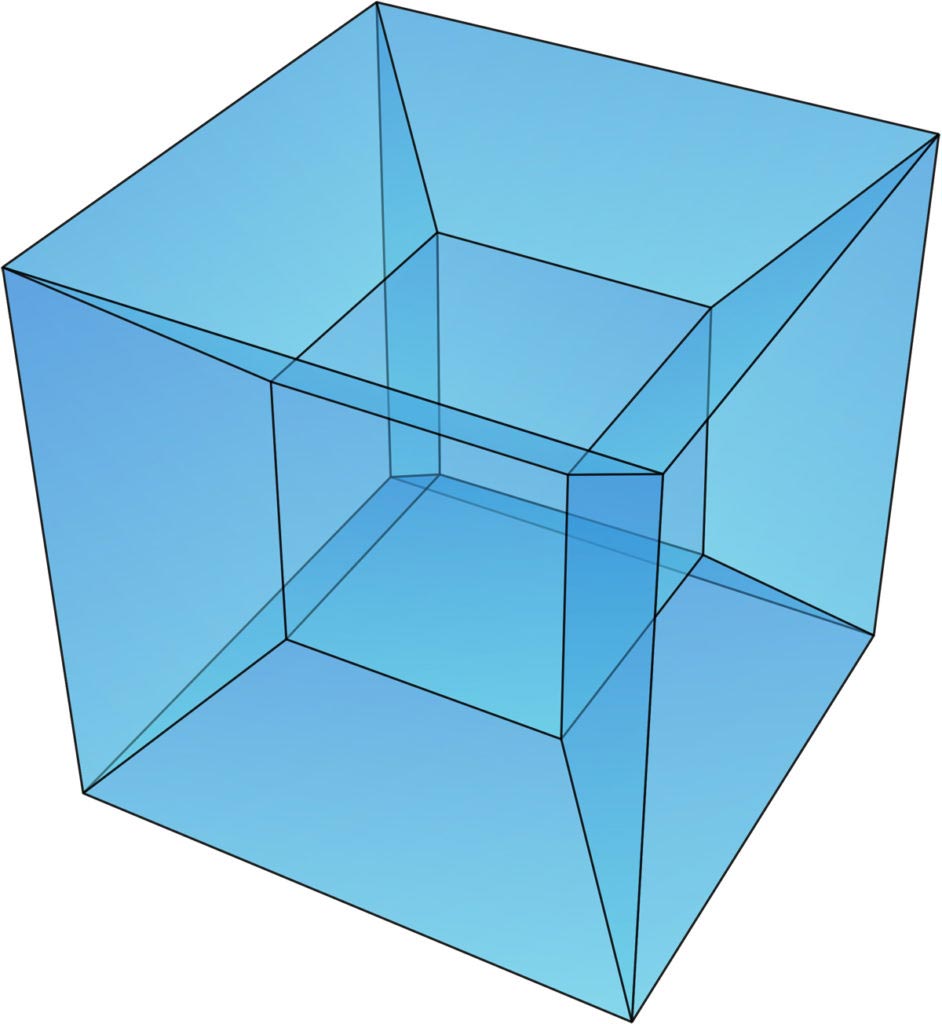
Ma se adesso vi dicessi di fare la stessa cosa con il cubo e di creare un cubo in 4 dimensioni (quello che viene chiamato «Tesseratto»), come risolvereste il problema?

Per farlo dovreste prendere un cubo e traslarlo in una direzione perpendicolare a se stesso, come abbiamo fatto con il quadrato; ma farlo è impossibile, perché non abbiamo una «quarta dimensione» verso cui traslare il cubo.

Dal punto di vista visuale, materiale, un Tesseratto non può essere costruito. Dal punto di vista matematico, invece, possiamo descrivere un cubo in infinite dimensioni ed è un oggetto geometrico a cui è stato dato un nome preciso: ipercubo.

Questo esempio ci è utile per introdurre l’argomento. Di seguito, infatti, proveremo a immaginare quale sarebbe il nostro punto di vista se fossimo creature abitanti in un universo con 1, 2, 3 e 4 dimensioni (e oltre). Teniamo sempre a mente la storia dell’ipercubo: noi abitanti della terza dimensione non possiamo vedere né immaginare correttamente un cubo costruito in quattro dimensioni.

L’articolo è un po’ lungo, perché cercherò di entrare il più possibile nei dettagli nel tentativo di immaginare i vari universi. Se lo trovate troppo lungo, spezzatelo in due letture; prendetelo come un esercizio di pensiero laterale.

Un viaggio attraverso le prime tre dimensioni

Nel trattare l’argomento ci verrà in aiuto Flatlandia, un famoso e particolare racconto scritto da Edwin A. Abbott che vi invito a leggere. Nel racconto, Abbott immagina un mondo fatto di due dimensioni, abitato da figure geometriche (ovviamente piane, perché esistono solo l’altezza e la larghezza). Il protagonista è un quadrato che si ritrova a viaggiare prima nell’universo a 1 dimensione e poi in quello a 3 dimensioni.

L’uso di figure geometriche nel racconto non è fatto per questione di “infantilismo”, ma perché è il modo più semplice per capire il concetto. Partendo dalle figure geometriche, comunque, possiamo arrivare anche a oggetti più complessi: noi umani, per esempio, possiamo immaginarci come un insieme di figure geometriche irregolari.

Per renderci conto della situazione, simuleremo di essere un quadrato che viaggia attraverso le dimensioni spaziali.

Prima di proseguire facciamo un breve ripasso di geometria, in modo da marcare alcuni concetti:
– L’elemento più piccolo in geometria è il punto, che possiamo definire rozzamente come «il più piccolo segno lasciato dalla punta di una matita». Intuitivamente, è un oggetto che non ha dimensioni fisiche [Dimensione 0].
– Se accostiamo almeno due punti, però, otteniamo una linea retta, cioè un elemento dotato di una sola dimensione [Dimensione 1, dove abbiamo solo la lunghezza].
– Concatenando vari punti vicini o varie linee, creiamo le figure geometriche piane: quadrati, pentagoni, cerchi [Dimensione 2: lunghezza e larghezza].
– Infine, traslando le figure di due dimensioni creeremo le figure tridimensionali: cubi, piramidi, sfere [Dimensione 3: lunghezza, larghezza e altezza].

Flatlandia: il mondo a 2 dimensioni [lunghezza e larghezza]

Partiamo dall’universo a 2 dimensioni, che è il più intuitivo da capire. Flatlandia è proprio il nome che Abbott attribuisce al mondo in cui esistono soltanto due dimensioni. In Flatlandia tutto è “piatto”, non ha un’altezza, per cui le regole sono molto diverse rispetto alle nostre.

Come riconoscere i vostri amici e famigliari

Immaginate di essere un quadrato di Flatlandia. Come fate a riconoscere le altre persone che vi circondano? Se ci pensate bene, riconoscere gli altri a vista non è così scontato, perché qualsiasi figura (persona) vi venga incontro, per voi avrà l’aspetto di una linea. Per capire cosa intendo, prendete due oggetti molto diversi tra loro – per esempio un libro e un pallone – e metteteli su un tavolo, poi abbassatevi con la testa all’altezza del tavolo e guardateli. L’unica cosa che potete vedere di loro è la lunghezza, cioè una linea.

Naturalmente, mentre il libro sarà una linea esatta, il pallone (un cerchio) sarà una linea “storta” e quindi le sue due estremità saranno più sfumate rispetto a quelle del libro. In Flatlandia, lo studio di queste sfumature è uno dei modi per riconoscere se si ha davanti un quadrato, un esagono, un cerchio o qualsiasi altra figura. Quindi la vista non è l’elemento più importante in Flatlandia: meglio affidarsi alla voce o al «tastarsi» per riconoscere un vicino.

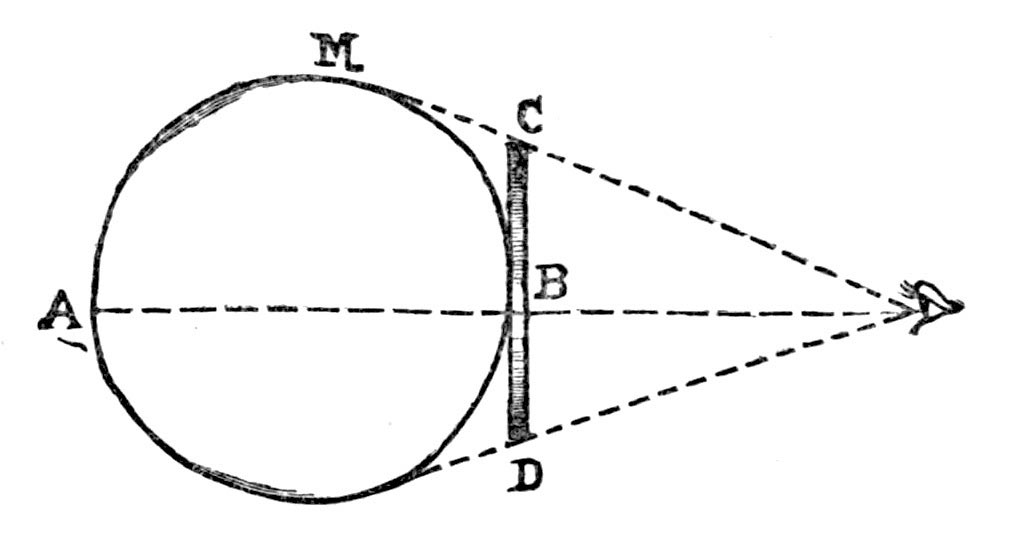
Una puntualizzazione importante. In un mondo così «piatto» non sarebbe nemmeno possibile vedere una figura dal davanti, per il semplice fatto che non ha nemmeno un cenno di altezza. L’unico modo per vedere una creatura del genere è di osservarla dall’alto – cosa che non potete fare, perché essendo voi un quadrato di Flatlandia non avete l’idea del «sollevarvi da terra». Le uniche direzioni che conoscete sono nord-sud ed est-ovest, ma non basso-alto.

Abbott risolve la questione specificando che ogni figura è dotata di una lucentezza e che quindi ci si può accorgere della sua presenza.

In questo mondo sono presenti anche le creature-linee: sarebbero elementi a una sola dimensione, dotati solo della lunghezza, ma in Flatlandia possono muoversi a destra e a sinistra, oltre che a nord e a sud: per cui sono da considerarsi linee dotate di una larghezza così minuscola da non essere visibile quando si mettono di lato (ma hanno pur sempre un accenno di larghezza).

L’arrivo di una sfera, abitante in tre dimensioni

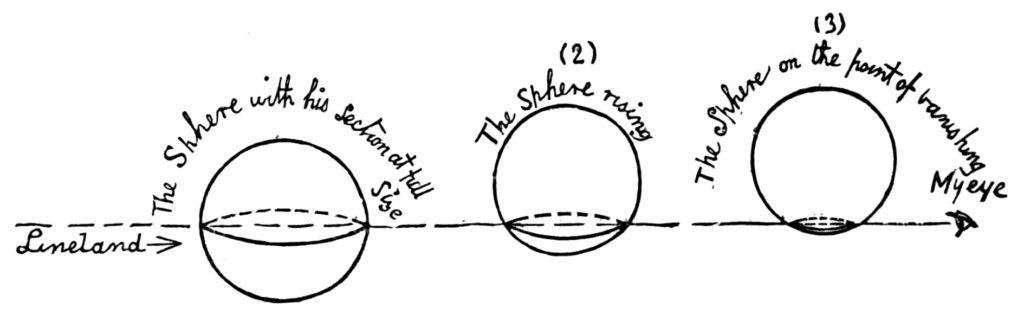
Voi, un quadrato, state camminando per strada e ad un certo punto vi appare improvvisamente la sagoma di un cerchio. Questo cerchio, però diventa sempre più grande, fino a raggiungere una circonferenza enorme. Dopodiché, diminuisce sempre più il suo raggio fino a scomparire nel nulla, così come era apparso.

Cos’è successo? Avete appena assistito all’ingresso di una sfera in Flatlandia. La sfera si è semplicemente limitata a salire dal basso, attraversando il vostro piano piatto (il vostro mondo) e scomparendo poi in alto. Il concetto diventa più chiaro se guardate l’immagine sopra. Voi non avete il concetto di «altezza» e i vostri occhi vedono solo dritto: per cui vi accorgete soltanto della sezione della sfera che interagisce con Flatlandia. Quando la sfera è per metà in Flatlandia, mostra il suo equatore, cioè il punto in cui la sua circonferenza è massima; salendo ancora, la circonferenza diminuirà.

Per voi è un fatto assurdo, incomprensibile, forse un trucco magico. Ancora più assurda, però, è la spiegazione che la sfera cerca di darvi: proviene da un mondo fatto di 3 dimensioni, chiamato Spacelandia. Purtroppo non ha nessun modo di spiegarvi come è fatta la terza dimensione, perché l’unico modo per farlo è di parlarvi di un «alto e basso», di cui voi non avete nessun concetto.

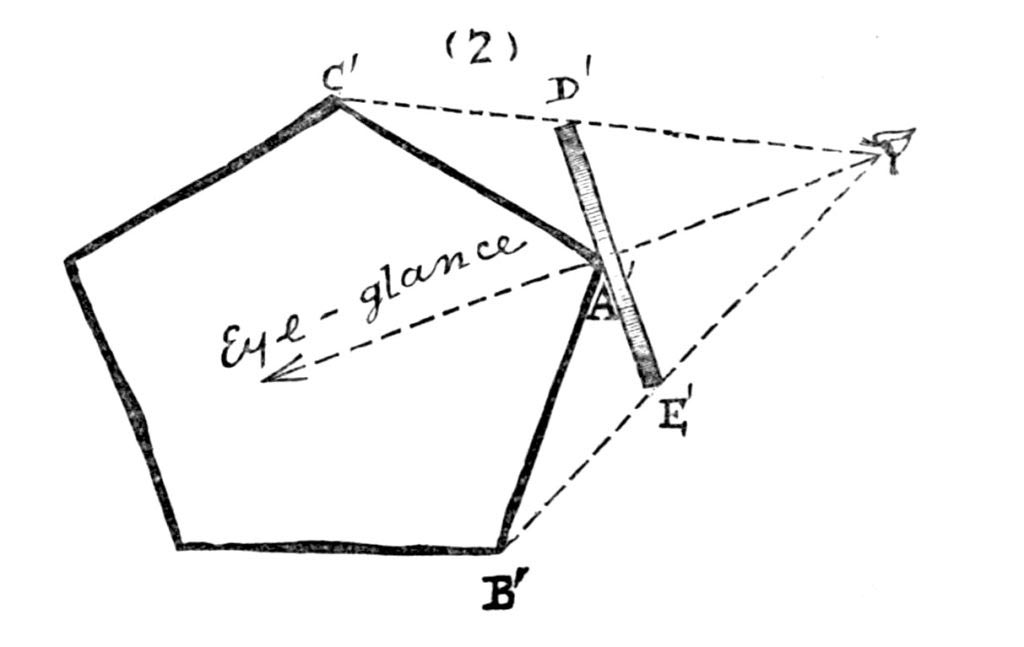
Cerca allora un altro approccio: per dimostrarvi che non sta mentendo, vi spiega che riesce a vedere l’interno del vostro corpo e tutti gli abitanti di Flatlandia fino a dove arriva il suo sguardo. Alla sfera, infatti, basta un’occhiata dall’alto e può vedere l’intero perimetro e superficie di linee, quadrati, pentagoni e cerchi.

Il risultato, però, è peggiore del primo. L’idea di poter guardare l’interno delle persone è per voi assurda, impossibile, e tra l’altro viola la vostra intimità. La normale reazione è che si tratti di un trucco ben congegnato che non sapete spiegarvi.

Linelandia: il mondo a 1 dimensione [lunghezza]

Per capire cosa intendesse dire la sfera, la vostra forma di quadrato scende in un mondo inferiore: Linelandia, dove esiste soltanto il concetto di «lunghezza». In pratica, il mondo è una linea retta infinita.

In questo caso, la situazione si inverte: siete voi a vedere gli abitanti sotto un punto di vista che loro non riuscirebbero mai a concepire. Gli abitanti, infatti, sono una sfilza di linee e di punti che si muovono avanti e indietro lungo un mondo “dritto, lineare”. Oltretutto, gli abitanti avranno sempre gli stessi vicini, per tutta la vita, perché non potranno mai sovrapporsi (non esiste né una larghezza né un’altezza che permetta di sorpassare o scavalcare il vostro vicino).

Qualsiasi tipo di rapporto si basa esclusivamente sul suono, sulla voce, perché il tatto come elemento di riconoscimento perde di significato quando per tutta la vita avrete sempre e comunque le stesse persone accanto.

Il loro movimento è da nord a sud e viceversa, mentre voi normalmente potete muovervi anche da est a ovest. Com’era successo per la sfera, però, voi diventate visibili soltanto per quella parte del vostro corpo che sta attraversando Linelandia; e il vostro aspetto risulterà quello di una linea.

E com’era successo per la sfera, ogni vostro tentativo di spiegare il significato di «larghezza» a un abitante si tradurrà in un nulla di fatto, anzi in un’irritazione: perché non appena spiegherete all’abitante che riuscite a vedere la sua lunghezza, significa che riuscite a vedere dentro il suo corpo, violando la sua intimità.

Pointlandia: il mondo senza dimensioni

Può esistere un universo senza dimensioni? Se ci affidiamo alla logica e alla geometria, deve esistere, perché una linea retta (che ha un’unica dimensione) non è l’elemento più elementare che conosciamo: si tratta infatti di un oggetto composto da un’infinità di punti.

Per raggiungere il mondo dove abita «il punto», dobbiamo scendere di un livello, ovvero in un universo senza dimensioni.

A questo punto entriamo più nella filosofia che nel pensiero razionale, perché un universo senza dimensioni è sinonimo del nulla – e dal nulla non può nascere «un qualcosa». È una questione al momento irrisolvibile per la scienza, perché è come chiedersi di cosa sia fatto l’elemento di base che va a formare gli atomi, le molecole e tutta la materia di cui è costituito il nostro universo, noi compresi.
Ma per lo scopo del nostro viaggio immaginario, non possiamo tralasciare quest’ultimo tassello.

Pointlandia è un universo davvero insolito. Esiste un solo abitante, un punto, che non conosce nient’altro al di fuori di se stesso. Riporto direttamente un passo del libro, che spiega ottimamente il suo possibile punto di vista:

Quel Punto è un Essere come noi, ma confinato nel baratro adimensionale. Egli stesso è il suo Mondo, tutto il suo Universo; egli non può concepire altri fuor di se stesso: egli non conosce lunghezza, né larghezza, né altezza, poiché non ne ha esperienza; non ha cognizione nemmeno del numero Due; né ha un’idea della pluralità, poiché egli è in se stesso il suo Uno e il suo Tutto, essendo in realtà Niente.

L’abitante-punto parla di se stesso in terza persona. Può riferirsi soltanto a se stesso, perché non esiste nient’altro nel suo mondo. Se voi, un quadrato, provate a parlargli, l’abitante crederà che la voce sia l’effetto di un suo pensiero: infatti come potrebbe un suono venire dal di fuori, dato che il «fuori» non esiste?

Il mondo a 4 dimensioni: come lo percepiamo?

Per concludere questo viaggio, torniamo alla realtà nel nostro corpo tridimensionale e cerchiamo di immaginare un universo fatto di 4 dimensioni spaziali. Questo universo avrà le nostre tre dimensioni – lunghezza, larghezza e altezza – più una quarta dimensione che chiameremo per semplicità “ALTEZZA4” (cioè l’altezza della quarta dimensione).

A inizio articolo vi avevo chiesto di immaginare un cubo e di traslarlo (spostarlo in perpendicolo) verso ALTEZZA4, in modo da creare un Tesseratto, cioè un cubo costruito in 4 dimensioni.

Immaginate che questo Tesseratto visiti il nostro universo. Quando si presenterà a noi, lo vedremo con l’aspetto di un cubo, perché le tre dimensioni sono le uniche che riusciamo a percepire. Lui, però, ci spiegherà che il cubo che vediamo è solo un’infinitesima parte di lui, un pezzo di lui che sta momentaneamente transitando attraverso il nostro mondo.

Il concetto è lo stesso della sfera che ha visitato l’universo del quadrato: agli occhi di quest’ultimo, l’unica parte visibile della sfera era la circonferenza che interagiva con il suo piano piatto.

Quindi il Tesseratto è dotato di un corpo a noi non visibile. Ma come è fatto questo corpo?
Sebbene lui tentasse di spiegarcelo, non riusciremmo a capirlo né a immaginarlo. Se non abbiamo minimamente idea di dove sia situata la direzione di ALTEZZA4, non possiamo nemmeno immaginare come sia composto un corpo fatto di 4 dimensioni.

Ma c’è di più: se ricordate bene, la sfera riusciva a vedere il quadrato dall’alto, cioè riusciva a vedere l’interno del suo corpo senza aprirlo. Per induzione, possiamo affermare che un Tesseratto riuscirebbe a vedere all’interno del nostro corpo semplicemente guardandolo dall’alto di ALTEZZA4.

Conclusione: mondi superiori alla quarta dimensione e la questione del tempo

La difficoltà di immaginarsi un mondo composto da 4 dimensioni spaziali ci mette davanti a un problema arduo da risolvere: non è possibile descrivere qualcosa di cui non abbiamo la minima percezione. Anzi, la nostra mente riesce a immaginare con difficoltà anche universi di 2 dimensioni, nonostante abbiamo una chiara percezione dell’idea di altezza e larghezza.

Il quadrato, per esempio, non è dotato di altezza. La vostra mente immagina che debba per forza esistere uno strato sottilissimo di altezza, perché altrimenti la forma che vedete dall’alto non potrebbe esistere, ma in realtà non è così: una figura bidimensionale non può essere dotata nemmeno di uno “strato sottilissimo”.

Per noi creature di tre dimensioni, una figura di sole 2 dimensioni non ha senso di esistere, così come non ha senso di esistere una figura di 4 dimensioni.

La difficoltà si accresce a ogni dimensione spaziale successiva: se prendiamo un Tesseratto e aggiungiamo un’ALTEZZA5, abbiamo un «Penteratto»; aggiungendo un’ALTEZZA6 creiamo un «Esseratto» e così via.
La teoria delle stringhe prevede l’esistenza di almeno 10 dimensioni spaziali e si tratta di un’ipotesi sempre più consolidata, per cui dovremmo cominciare ad abituarci all’idea che attorno a noi, in qualche forma non ben comprensibile, esistano delle altre profondità spaziali. Anzi, il nostro stesso corpo “galleggerebbe” attraverso queste dimensioni senza che ne abbiamo la minima percezione.

Un accenno sul tempo

Accenno poi a un’altra questione, senza svilupparla. Sappiamo che il tempo e lo spazio sono strettamente legati, in quello che definiamo spaziotempo. Se si deforma l’uno, si deforma anche l’altro (se vi sfugge questo concetto, date un’occhiata all’articolo sulla relatività generale).

Considerata questa connessione, ci possiamo chiedere come percepisca il tempo un abitante della quarta o della quinta dimensione. Alcune teoria accennano all’idea che essendo libere di muoversi in direzioni diverse nello spazio, sono libere di muoversi anche in direzione diverse nel tempo.

In altre parole, se un abitante della dimensione 4 scendesse nella dimensione 3, potrebbe essere capace di viaggiare in avanti e indietro nel tempo a piacere.

A parte la questione etica («se è in grado di muoversi avanti e indietro a piacere, significa che la nostra linea temporale è già completamente prestabilita?»), l’idea ci pone alla mente un’altra domanda: «se comprendiamo il funzionamento delle dimensioni superiori, saremo in grado di viaggiare nel tempo?».

La sentenza alle generazioni future, probabilmente, perché per adesso siamo ancora ben lontani dal ricevere una risposta chiara e scientifica.